Na tarde de domingo, o Matix estava a brincar com peças quadrangulares de um jogo e, com 10 peças construiu um retângulo, como se vê na figura.

Ao observar a construção, pensou logo num desafio para fazer ao seu Pai.

“Sabendo que as medidas dos lados dos quadrados são os menores números naturais possíveis, determina o valor da área da construção”.

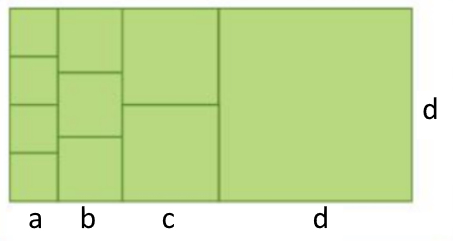Observação: Na figura o valor do lado de cada quadrado está representado por uma letra.

Ajuda a Pai do Matix a resolver o desafio e, explicando como pensaste, descobre a área do retângulo da figura.

Resposta da equipa “5×5=?”

A área do retângulo da figura é 300. 25×12=300.
Se o quadrado a fosse 1, a altura d seria 1×4=4. Então b seria 4÷3 mas não dava número natural. Então se a fosse 2, altura d seria 2×4=8, logo b seria 8÷3, também não dá número natural.
Se a fosse 3, a altura d seria 3×4=12. Então b seria 12÷3=4 ja é número natural. A seguir letra c é 12÷2=6. A letra d 12÷1=12. Depois é só somar 3+4+6+12=25. A altura d 3×4=12. A área dá 25×12=300.

Resposta da equipa “Os matemãticos”

Primeiro tentámos fazer as tabuadas do 4, do 3 e do 2 para descobrirmos o número que esteja nas três tabuadas. Descobrimos que era o d=12, 0 c=6, o b=4 e 0 a=3, somamos todos e deu 25. então 25×12=300
A área do retângulo é 300

Resposta da equipa “peúgas”

Escrevemos os múltiplos de 2; 3 e 4 e descobrimos que o múltiplo comum era 12, que correspondia à letra D porque 12 é divisível por 4; 3 e 2. Descobrimos que a letra C correspondia a 6cm porque 6 cabe 2 vezes no 12 cm, a letra B correspondia a 4 cm porque 4 cm cabe 3 vezes mo 12 cm e a letra A correspondia a 3 cm porque 3 cm cabe 4 vezes no 12 cm. Por fim multiplicámos o comprimento pela largura, ou seja multiplicámos 25 cm por 12 cm, o que nos deu um resultado de 300 cm2.

Resposta da equipa “TEST C9”

A área do retângulo é 300. Nós tentamos usar os menores números a, b, c, d e usamos 1,2,3,4 e descobrimos que não batia certo.
Depois fomos procurar o menor número que estivesse nas tabuadas do 4 ,do 3 , do 2 e do 1
encontrámos o 12 . Assim o valor do lado dos 4 quadrados menores (a) era 3 (12 : 4 = 3) ; o valor do lado dos 3 quadrados 4 (12 : 3 = 4 ) ; o valor do lado dos 2 quadrados (c) era 6 (12 : 2 = 6 ) e do quadrado grande era 12 . Calculámos a área dos diferentes quadrados e obtivemos a área do retângulo que era 300 (9+9+9+9+16+16+16+36+36+144 = 300).